Data una matrice 6 x 6, una clessidra (hourglass)è un sottoinsieme di elementi della matrice che rispettano il pattern mostrato in figura:

In una matrice 6 x 6 si possono individuare 16 clessidre. La somma di una clessidra è la somma di tutti gli elementi appartenenti ad essa. Trova la massima somma di tutte le clessidre presenti nella matrice. 

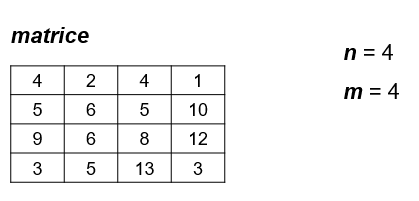
Ad esempio per la matrice:

si possono individuare 16 clessidre le cui somme sono:

Ritornare la massima somma è 28 ovvero quella corrispondente alla seguente clessidra:

Analisi del problema

Per poter risolvere il problema è necessario per prima cosa effettuare una fase di analisi che ci aiuti a comprenderlo bene. La funzione da progettare deve prendere in input una matrice 6×6 e deve restituire la massima somma fra le clessidre contenute in essa. Possiamo scrivere la signature della funzione che è la seguente:

def hourglassSum(matrix):

A questo punto possiamo elaborare una soluzione per il problema. E’ possibile verificare che all’interno di una matrice 6 x 6 si possono individuare 16 clessidre ovvero 4 per ogni riga fino alla quarta riga. Per la prima riga ad esempio le clessidre sono:

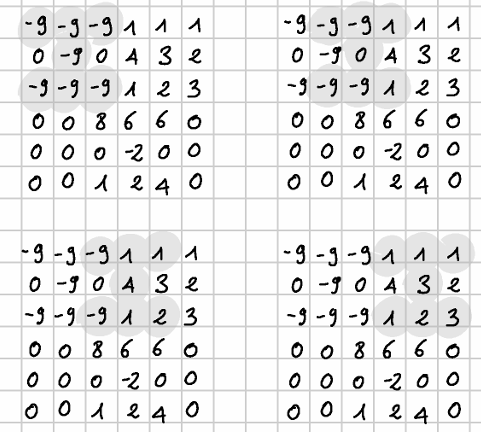
L’ultima clessidra che è possibile individuare è:

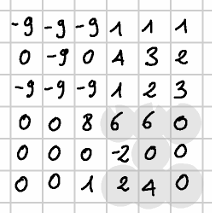
Per ogni clessidra che consideriamo è possibile calcolare la somma dei suoi elementi:

Possiamo calcolare quindi la somma di ogni clessidra e inserirla in un vettore del quale calcoleremo in seguito il massimo.

Progetto

Resta ora una domanda fondamentale: come fare ad individuare ogni clessidra (hourglass)? L’idea è quella di creare un indice i che scorre le righe dalla 0 alla 3 (ovvero l’ultima riga sulla quale può partire una clessidra) e un indice j che scorre per le colonne dalla 0 alle 3 per trovare il primo elemento dal quale calcolare l’intera clessidra:

for i in range(4):
        for j in range(4):
            s = arr[i][j] + arr[i][j+1] + arr[i][j+2] + arr[i+1][j+1] + arr[i+2][j]+arr[i+2][j+1]+arr[i+2][j+2]

Una volta calcolata la somma degli elementi è necessario inserirla in un vettore in modo da avere tutte le somme delle quali trovare i massimo:

def hourglassSum(arr):
    vet = []
    for i in range(4):
        for j in range(4):
            s = arr[i][j] + arr[i][j+1] + arr[i][j+2] + arr[i+1][j+1] + arr[i+2][j]+arr[i+2][j+1]+arr[i+2][j+2]
            vet.append(s)
            
    m = vet[0]
    for s in vet:
        if s > m:
            m=s
    
    return m
    

https://www.hackerrank.com/challenges/2d-array/problem

Torma a matrici