La logica proposizionale fornisce uno strumento potente per analizzare il rapporto tra idee e proposizioni, e le connessioni logiche sono il filo conduttore che dà vita a questa forma di ragionamento formale.
Le espressioni logiche costituiscono il linguaggio fondamentale della logica proposizionale. Ogni espressione logica è composta da proposizioni atomiche, variabili proposizionali e connettivi logici. Le proposizioni atomiche rappresentano dichiarazioni elementari, mentre le variabili proposizionali fungono da segnaposto per proposizioni specifiche.
Attraverso l’esplorazione degli operatori logici fondamentali – congiunzione, disgiunzione, implicazione e bicondizionale – scopriremo come le proposizioni semplici si legano l’una all’altra per formare strutture argomentative significative. La congiunzione, rappresentata dal simbolo ∧, unisce idee in modo coeso, mentre la disgiunzione (∨) permette di esprimere alternative. L’implicazione (→) ci guida attraverso il terreno della deduzione logica, mentre il bicondizionale (↔) svela relazioni di equivalenza.
I tre principali connettivi logici sono AND, OR e NOT.
And
Il connettivo logico AND, rappresentato come ∧, esprime l’idea che due proposizioni siano vere contemporaneamente. La tavola di verità per l’AND è la seguente:
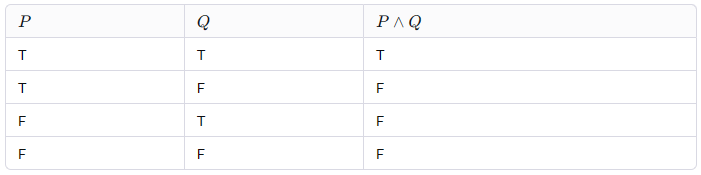
L’espressione P∧Q è vera solo quando entrambe P e Q sono vere. Un esempio di combinazione di due proposizioni con la and è il seguente:
Proposizioni Semplici:
- p: Il sole è splendente.
- q: Il cielo è azzurro.
Congiunzione: p∧q
- Il sole è splendente e il cielo è azzurro.
Ecco un altro esempio
- v: Il numero è pari.
- w: Il numero è maggiore di 10.
Congiunzione: v∧w
- Il numero è pari e il numero è maggiore di 10.
Or
Il connettivo logico OR, rappresentato come ∨, esprime l’idea che almeno una delle proposizioni sia vera. La tavola di verità per l’OR è la seguente:
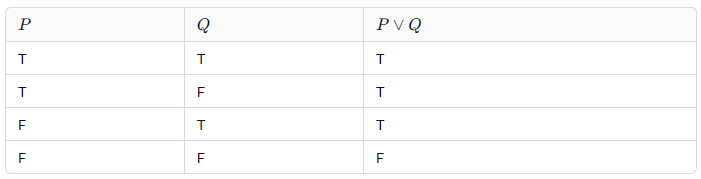
L’espressione P∨Q è falsa solo quando entrambe P e Q sono false. Ecco un possibile esempio:
Proposizioni Semplici:
- p: Il sole è splendente.
- q: Piove.
Disgiunzione: p∨q
- Il sole è splendente o piove.
Not
Il connettivo logico NOT, rappresentato come ¬, nega una proposizione. La tavola di verità per il NOT è la seguente:

L’espressione ¬P è vera quando P è falsa e viceversa.
Implicazione
L’implicazione logica è uno degli operatori fondamentali della logica proposizionale, giocando un ruolo cruciale nell’analisi del ragionamento e nella costruzione di argomentazioni valide.
L’implicazione logica, spesso rappresentata con il simbolo “→”, collega due proposizioni, di solito indicate come p e q. L’implicazione p→q afferma che se la proposizione p è vera, allora la proposizione q deve anch’essa essere vera. Tuttavia, non implica nulla riguardo la verità di p quando q è falsa.

L’implicazione possiede alcune proprietà importanti:
- Trasitività: Se p→q e q→r, allora p→r.
- Contrapposizione: Se p→q, allora ¬q→¬p.
- Legge di Sostituzione: Se p→q e p è vero, allora q deve essere vero.
La potenza della logica proposizionale risiede nella capacità di combinare questi connettivi per formare espressioni complesse. Ad esempio, consideriamo l’espressione (P∧Q)∨¬R. Per valutare questa espressione, applichiamo le regole dei connettivi logici in modo sequenziale.
Formule ben formate
Nella logica proposizionale, le “Formule Ben Formate” (FBF) svolgono un ruolo cruciale nel garantire la coerenza e la correttezza delle espressioni logiche. Una Formula Ben Formata è una sequenza di simboli che segue regole ben definite di sintassi, consentendo una rappresentazione chiara e inequivocabile di proposizioni. Le FBF sono costruite in base alle regole di formazione che definiscono come combinare variabili proposizionali, connettivi logici e simboli ausiliari in maniera accettabile. Le formule ben formate sono definite attraverso questa formula ricorsiva:
- un simbolo di proposizione è una fbf
- se A è una fbf lo è anche (¬A)
- se A e B sono fbf allora lo sono anche (A ∧ B), (A ∨ B), (A → B) e (A ↔ B)
- niente altro è una fbf
Inoltre i connettivi logici vengono eseguiti nel seguente ordine:
- ¬, ∧, ∨, →, ↔
quindi l’espressione p ∧¬ q è la formula (p ∧ (¬q)).
Torna a selezione