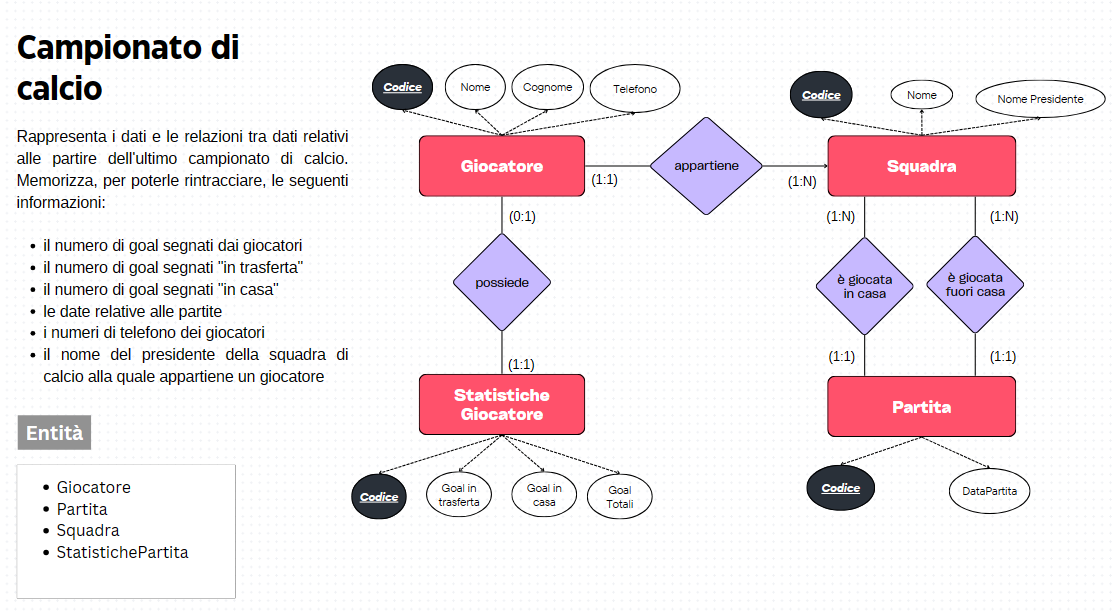
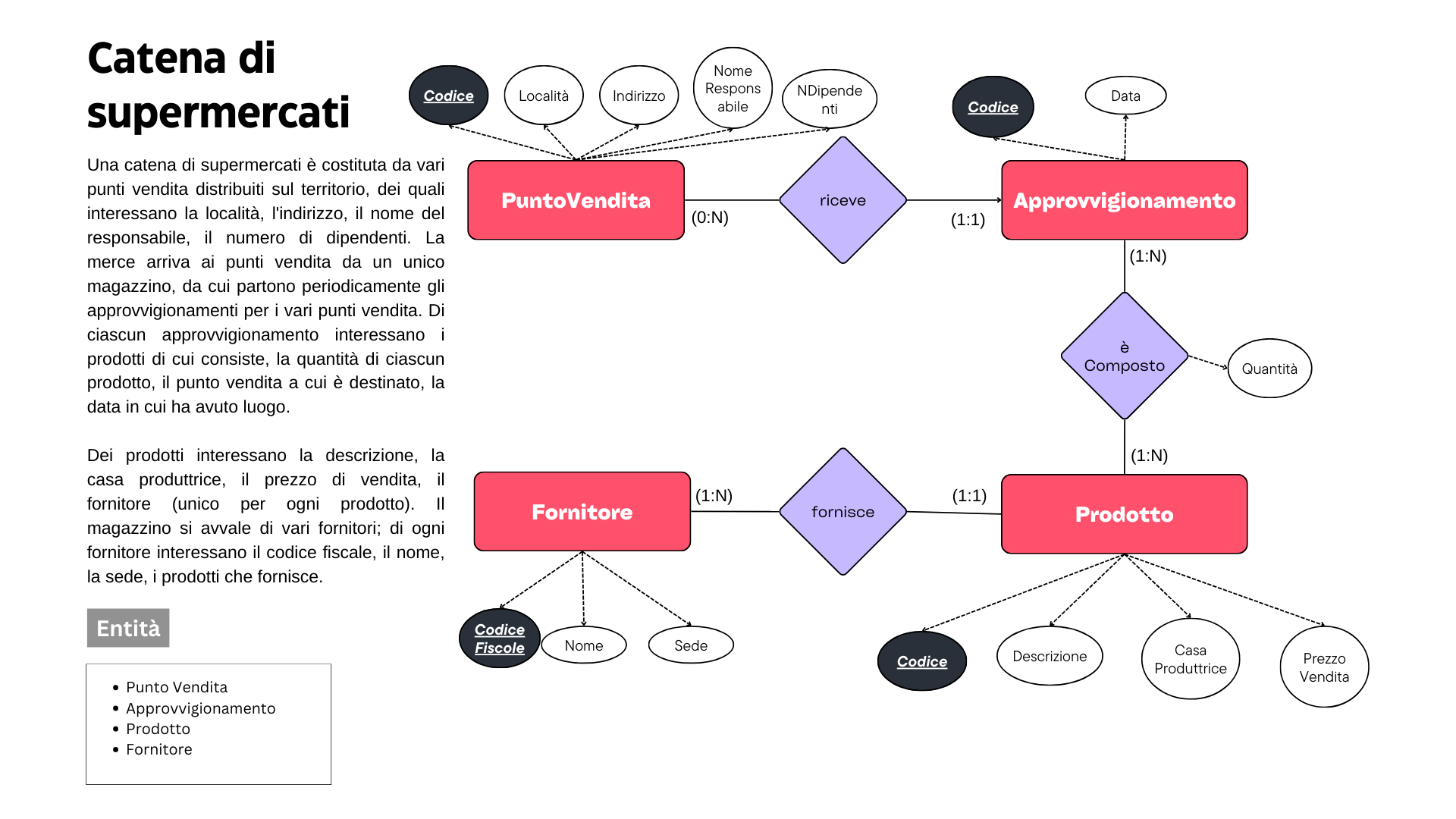
La regressione è un metodo statistico utilizzato per studiare la relazione tra una variabile dipendente (o risposta) e una o più variabili indipendenti (o predittori). È uno strumento fondamentale nell’analisi dei dati e viene impiegato in una vasta gamma di campi, tra cui l’economia, la psicologia, la biologia, la medicina, l’ingegneria e molti altri.
La regressione permette di prevedere valori continui. Quanto costerà questa casa !?
Supponiamo di avere dati relativi al prezzo di case in base a diverse caratteristiche come la dimensione della casa (in piedi quadrati), il numero di camere da letto e il numero di bagni. Vogliamo utilizzare la regressione per prevedere il prezzo delle case in base a queste caratteristiche.
Variabili dipendenti
Le variabili dipendenti sono il fulcro dell’analisi di regressione e rappresentano il dato da trovare. Sono le variabili che si cercano di spiegare o prevedere attraverso l’uso di altre variabili. In molti casi, le variabili dipendenti rappresentano il fenomeno che si sta studiando o che si vuole comprendere meglio.
Nell’esempio che stiamo considerando la variabile dipendente è il prezzo in quanto è il valore che vogliamo trovare. Le variabili dipendenti possono assumere diverse forme a seconda del tipo di analisi in corso:
- Variabili continue: Se la variabile di interesse è quantitativa e può assumere un’infinità di valori all’interno di un intervallo, si tratta di una variabile dipendente continua. Ad esempio, il reddito annuo di una persona, la temperatura giornaliera, ecc.
- Variabili discrete: Quando la variabile può assumere solo valori specifici e distinti, si parla di variabile dipendente discreta. Ad esempio, il numero di visite al medico in un anno, il numero di articoli venduti, ecc.
- Variabili categoriche: Queste sono variabili che rappresentano categorie o gruppi e non hanno un ordinamento intrinseco. Ad esempio, il colore degli occhi, la marca di un’auto, ecc.
Le variabili dipendenti svolgono un ruolo cruciale nell’analisi di regressione in quanto sono il focus principale dell’analisi. Il loro comportamento e la loro relazione con le variabili indipendenti determinano in gran parte la validità e l’utilità del modello di regressione.
- Spiegazione dei fenomeni: Le variabili dipendenti spiegano i fenomeni osservati o misurati. Ad esempio, in un modello di regressione che studia il rendimento accademico degli studenti, la variabile dipendente potrebbe essere il punteggio degli esami.
- Previsione: Le variabili dipendenti possono essere utilizzate per prevedere futuri risultati o comportamenti. Ad esempio, un modello di regressione potrebbe prevedere il prezzo di mercato di una casa basandosi sulle sue caratteristiche.
Variabili predittori
Le variabili predittori, anche chiamate variabili indipendenti o regressori, sono le variabili utilizzate per spiegare o prevedere la variabile dipendente. Queste variabili sono controllate o manipolate nel contesto dell’analisi per comprendere il loro impatto sulla variabile dipendente.
Le variabili predittori possono assumere diverse forme e possono essere di diversi tipi a seconda del contesto dell’analisi:
- Variabili continue: Variabili quantitative che possono assumere un’infinità di valori all’interno di un intervallo. Ad esempio, l’età di una persona, il reddito mensile, ecc.
- Variabili categoriche: Variabili che rappresentano categorie o gruppi e non hanno un ordinamento intrinseco. Ad esempio, il genere di una persona, il tipo di trattamento medico ricevuto, ecc.
Nel nostro caso possiamo utilizzare le variabili relative alla grandezza della casa, al numero di camere da letto che possiede e al numero di bagni.
Il modello regressivo dati in input i valori dei predittori ha lo scopo di calcolare il possibile risultato della variabile indipendente (prezzo):
Tipi di regressione lineare
La regressione lineare potrebbe essere semplice o multipla. Entrambe sono tecniche utilizzate nell’analisi per comprendere e modellare le relazioni fra la variabile di risposta e i predittori.
Nella regressione lineare semplice, c’è una sola variabile indipendente coinvolta ed utilizzata per predire la variabile dipendente. Un esempio chiave potrebbe essare un modello che permette di prevdere la vendita dei gelati in relazione alla temperatura. La relazione tra variabile indipendete e variabile dipendente è descritta nel piano da una retta.
Nella regressione multipla si coinvolgono più variabili indipendenti per il calcolo della risposta. Sicuramente questo modello è più complesso e la relazione fra le variabili indipendenti e la variabile dipendente è descritta da un iperpiano (un’estensione della retta in più dimensioni). Un esempio potrebbe essere un modello che utilizza temperatura, umidità e giorno della settimana per predire la vendita dei gelati.
Regressione Semplice
Supponiamo di avere dati relativi al numero di ore di studio e i punteggi ottenuti in un esame. Vogliamo utilizzare la regressione per prevedere il punteggio in base alle ore di studio.
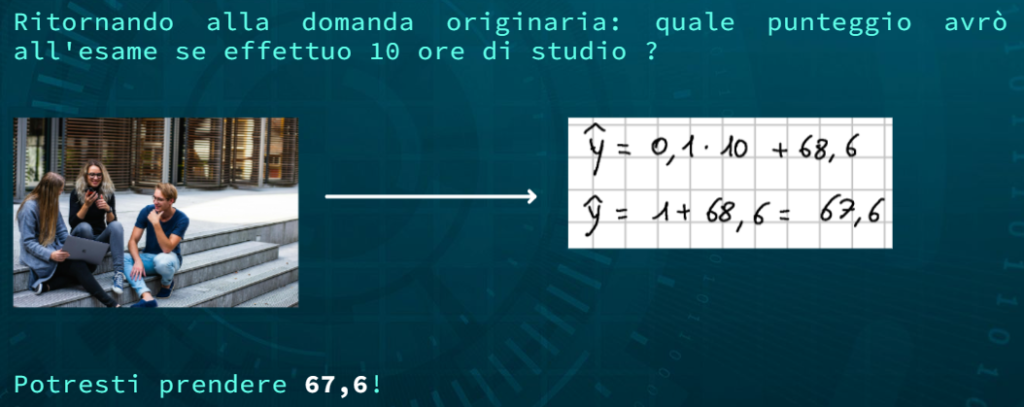
La regressione in questo contesto può permettere di rispondere ad esempio alla seguente domanda: “Quanto prenderò all’esame se studio 10 ore?”
Scatter Plot
Il primo passo per poter effettuare una regressione potrebbe essere quello di rappresentare i dati un sistema di assi cartesiani. In questo esempio le ore di studio rappresentano la variabile indipendente mentre il punteggio all’esame la variabile dipendente:
Per rappresentare i dati è possibile utilizzare la libreria Python matplotlib:
A questo punto il modello regressivo permetterà di individuare la retta che meglio approssima i dati che utilizzeremo come modello per effettuare nuove previsioni:
Sappiamo che l’equazione della retta in forma esplicita è:
dove 0 è l’ordinata all’origina mentre 1 è il coefficiente angolare della retta.
Metodo dei minimi quadrati
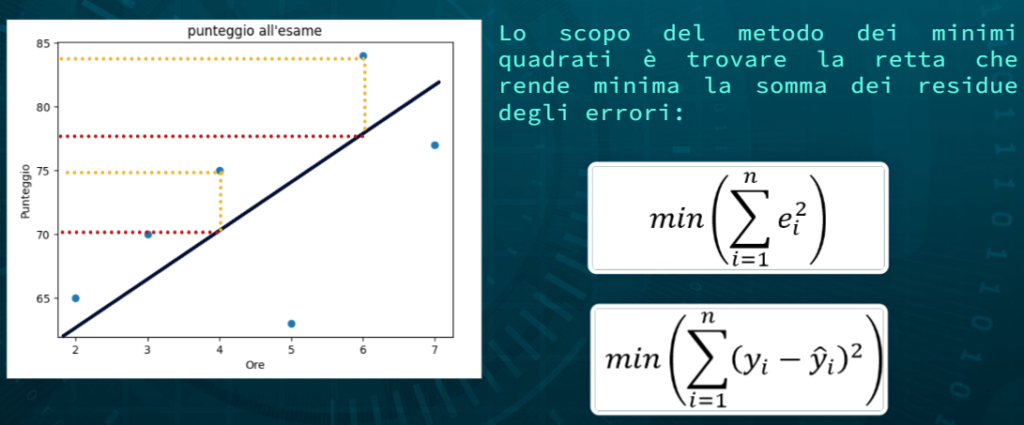
Il metodo dei minimi quadrati è un approccio utilizzato per adattare una linea (o un iperpiano) ai dati. Nella regressione lineare, ci concentriamo sul trovare una linea retta che meglio si adatta ai dati. Questo viene fatto minimizzando la somma dei quadrati delle differenze tra i valori osservati e quelli predetti dalla linea. Considerando il dataset precedente la retta che meglio approssima i dati potrebbe essere la seguente:
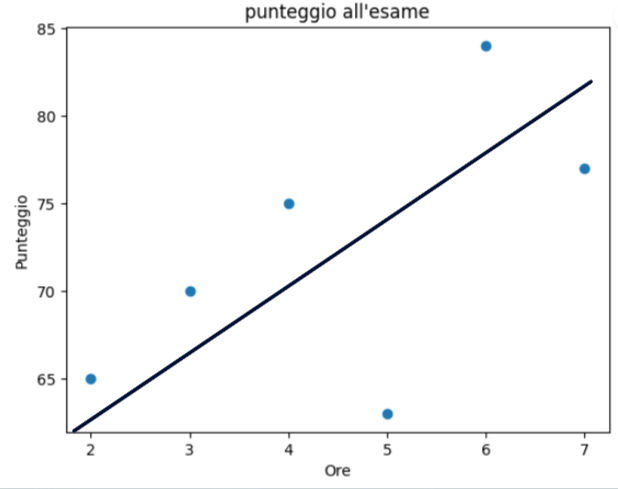
La linea retta può essere rappresentata da un’equazione nella forma:
![]()
Lo scopo dell’algoritmo di regressione lineare e trovare i coefficienti \Theta_1 (coefficiente angolare) e \Theta_0 che definiscono la retta che “meglio” approssima i dati. Ma cosa vuol dire approssimare meglio? Cerchiamo di dare una definizione un pò più formale. Poichè la retta è un modello, questa approssima i dati e quindi potrebbe essere possibile la presenza di errori. Facciamo un esempio:
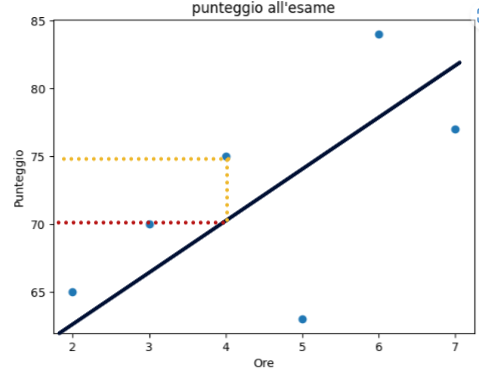
Considerando l’immagine precedente, con 4 ore di studio lo studente prende come punteggio 75. La funzione della retta invece restituirebbe punteggio 70. C’è quindi per questo singolo dato un errore misurabile di 5 unità. Definiamo errore quadratico il quadrato dell’errore per questo dato:
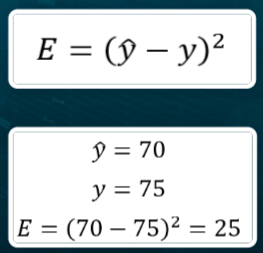
La nostra retta deve minimizzare l’errore quadratico rispetto ai punti del piano. In termini più semplici, consideriamo che abbiamo un insieme di punti di dati ![]() , dove
, dove ![]() rappresenta l’input (variabile indipendente) e
rappresenta l’input (variabile indipendente) e ![]() rappresenta l’output (variabile dipendente). Vogliamo trovare una linea retta che rappresenti al meglio la relazione tra
rappresenta l’output (variabile dipendente). Vogliamo trovare una linea retta che rappresenti al meglio la relazione tra ![]() e
e ![]() .
.
Dove ![]() rappresenta la pendenza della retta e
rappresenta la pendenza della retta e ![]() rappresenta l’intercetta sull’asse delle ordinate. Il metodo dei minimi quadrati cerca di trovare i valori ottimali di
rappresenta l’intercetta sull’asse delle ordinate. Il metodo dei minimi quadrati cerca di trovare i valori ottimali di ![]() e
e ![]() in modo che la somma dei quadrati delle distanze verticali tra i punti di dati e la linea sia minimizzata.
in modo che la somma dei quadrati delle distanze verticali tra i punti di dati e la linea sia minimizzata.
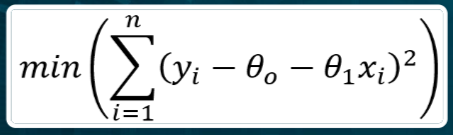
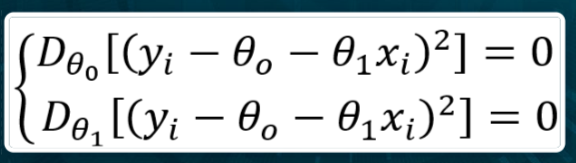
Se consideriamo \Theta_1 come variabile indipendente e sviluppiamo il quadrato, notiamo che l’andamento del coefficiente angolare rispetto all’errore è definito da una parabola nel piano:
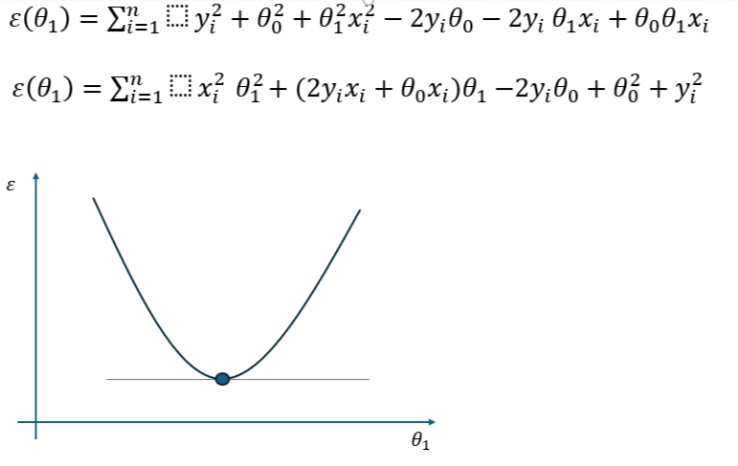
Minimizzare questa funzione significa trovare il punto di minimo cioè il valore di \Theta_1 nel quale l’errore è minimo. Per questo motivo è possibile derivare la funzione rispetto a \Theta_1 e porre il valore della derivata uguale a 0. Il risultato è la seguente formula per il calcolo del coefficiente angolare:
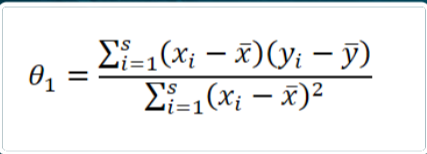
e della seguente per il calcolo dell’ordinata all’origine:
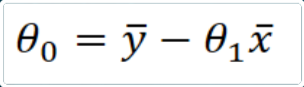
Per l’esercizio di esempio che permette di calcolare il voto presunto dopo uno studio di 10 ore i calcoli sono i seguenti:

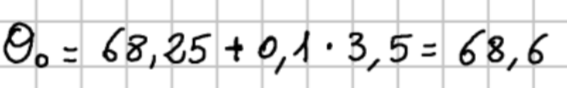
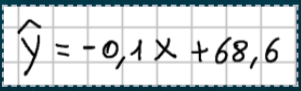
Torna a Intelligenza Artificiale